We’ve all been asked whether we’d prefer to have a million dollars or a chess board of pennies, where the number of pennies is doubled in each square. (For the mathematically inclined, we’re trying to figure out whether
1,000,000 is greater or less than 2^64
Those unfamiliar with compounding will select $1,000,000 and those who understand what 2^64 means will select the chess board of doubling pennies.
Some of us may also be familiar with “marginal gains” which was an approach to improvement (some highly effective, some dubious) British Cycling implemented for more than a decade.
Oversimplified, the goal was to try to be 1% better each day.
My high school volleyball coach taught us this a long time ago, but not till today did I see the effect mathematically. And it was only truly understood by seeing the compounding and reverse effects.
With a slight return to mathematical notation (within WordPress’s limitations…):
Let improvement or decline occur daily at a rate of 1% (0.01) for 365 days. And let no change be denoted as 1.0 These three situations can be represented by the following: No change 1.0^365 = 1 Decline 0.99^365 ≈ 0.0255 Improvement 1.01^365 ≈ 37.78
The bonkers part of this is there is a total of 0.02 difference between 0.99 and 1.01. Simply a day’s effort in the wrong direction.
Is every day actually + 0.01 or – 0.01? Probably not, but the message is clear:
Decline takes you asymptotically toward 0.00.
Improvement has no upper limit, and despite a long time of very little improvement, it is still exponential growth.
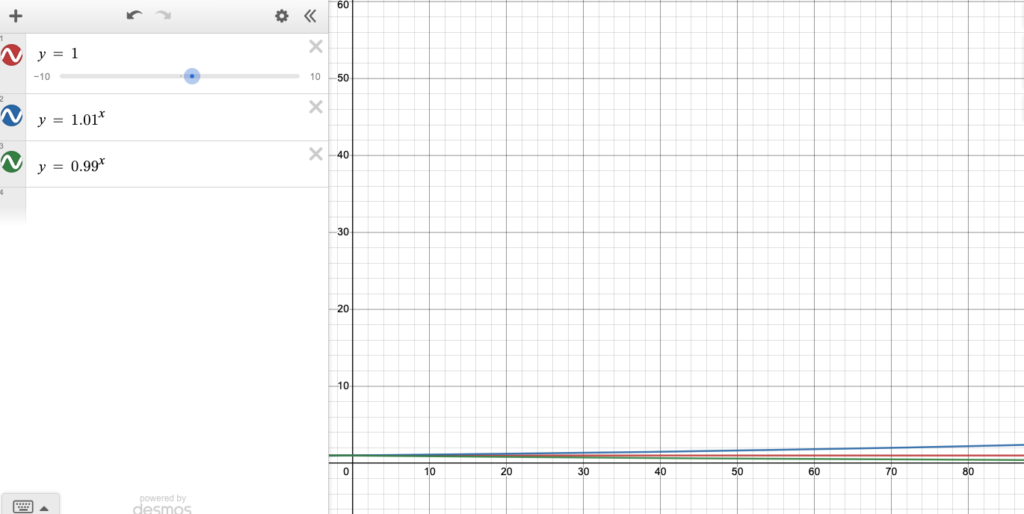
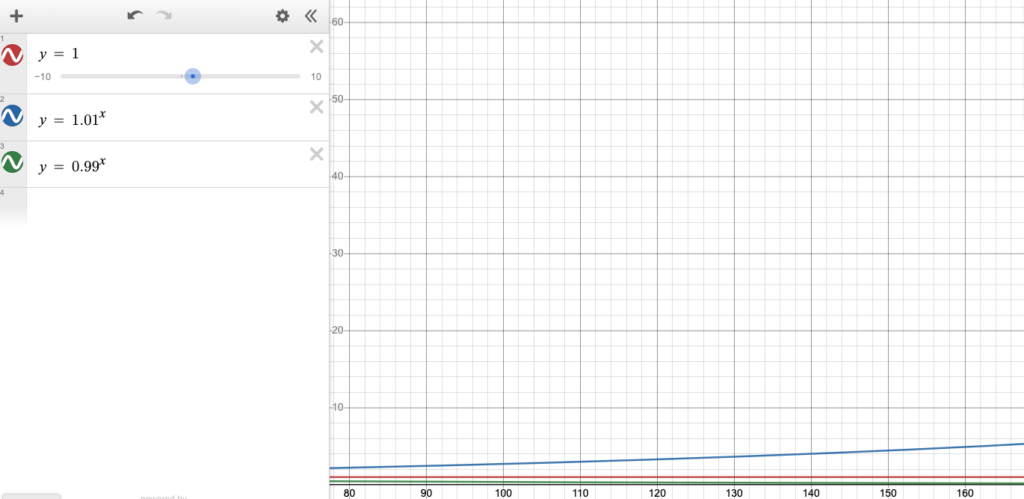
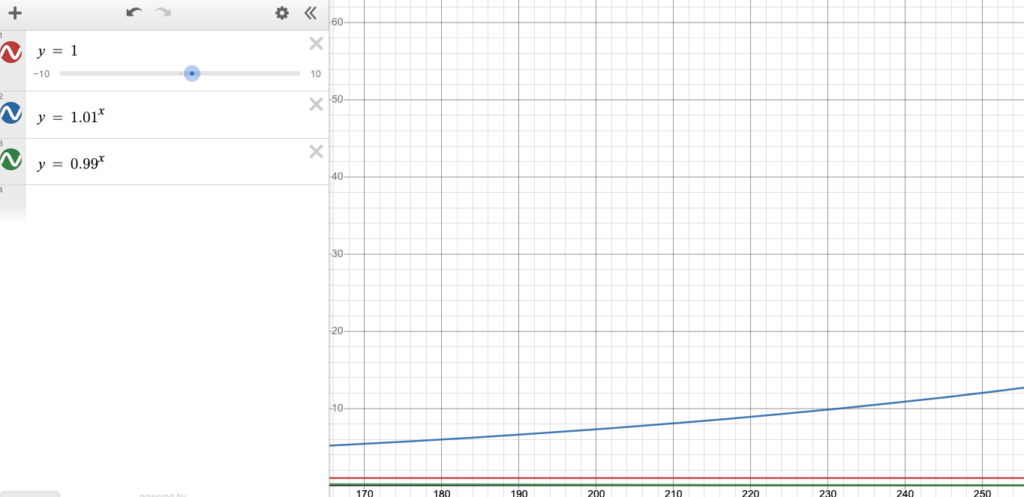
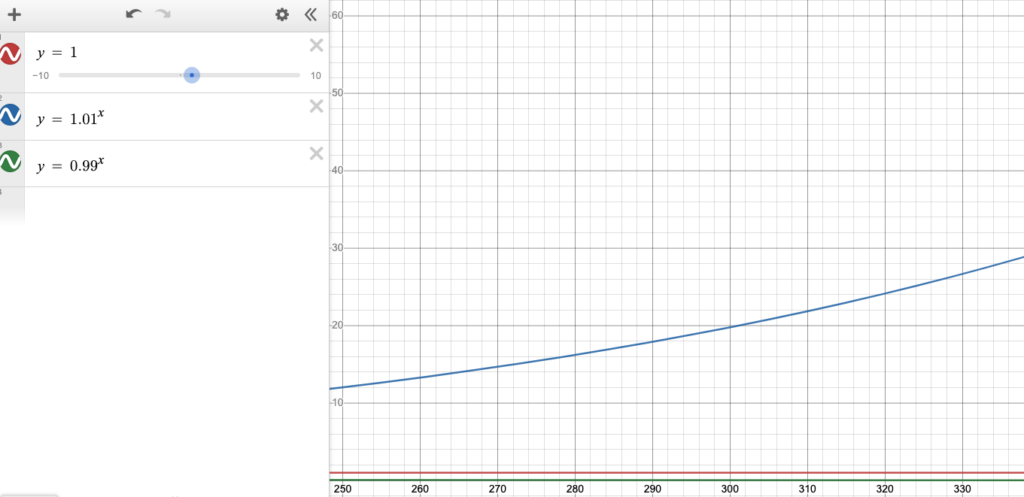
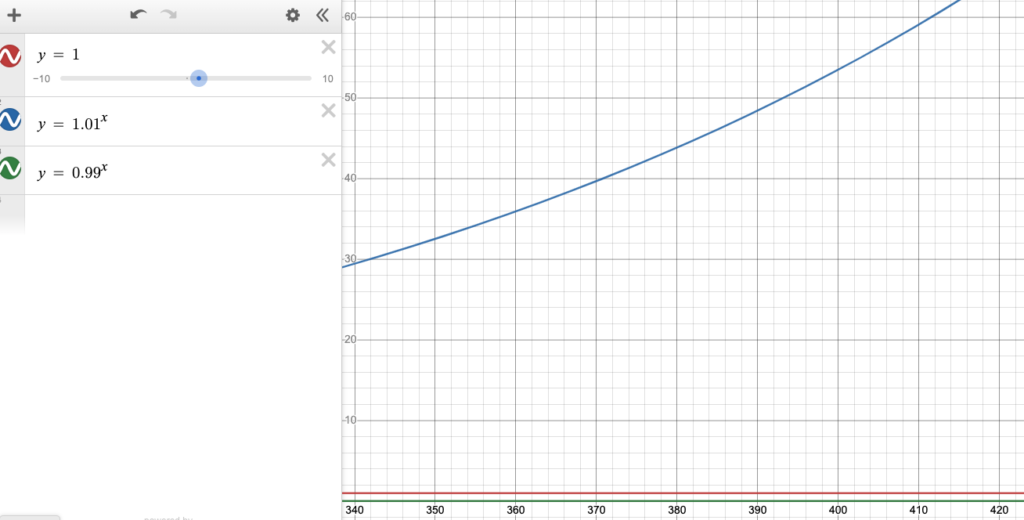
To attempt to show how long the effort takes to compound, consider the following screenshots of the lines
y = 1 y = 0.99^x y = 1.01^x
Yes, I’m sure you haven’t thought about this type of stuff since high school.
These all maintain the same Y axis. Notice it takes until 1.01^x, where x = 415 to get off the scale (y ≈ 62).
It’s also worth noting that there is a point where y = 1.01^x becomes larger than y = x (linear progression).
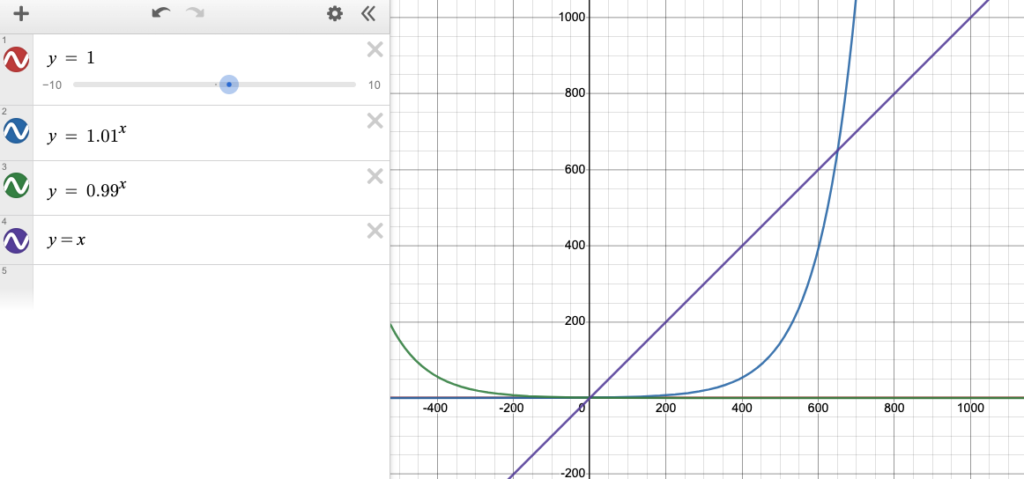
This is about at 620.
The point of this isn’t to hold the numbers to task. But the point is to demonstrate that exponential growth, even in minute amounts eventually outpaces linear growth.
And minute amounts of growth daily is possible.